200以上 75 15 üçgeni 242819

History Of Mathematics In The Turkish Middle School Mathematics Curriculum And Textbooks Semantic Scholar
DİK ÜÇGENİN ALANI Diküçgenin alanı, dik kenarların çarpımının yarısıdır WordPresscom'da bir web sitesi veya blog olu�90 75 15 Üçgeni, 90 75 15 Üçgeni Özellikleri ucgengentr img Math off the grid And yet more fun img Angle Sums and the Right Triangle – GeoGebra img #75 #90 Combo Embroidery Needles img 15 75 90 Triangle Side Lengths img triangle Math, Trigonometry, Right Triangles ShowMe
75 15 üçgeni
75 15 üçgeni-15 75 90 Üçgeni Üçgende Açılar Ders Notları Kunduz Angle Sums and the Right Triangle – GeoGebra Math off the grid Revisiting the Gebhard, Curt / PreCalc Notes135 üçgeni Bradley Kozey 485 Followers 135 üçgeni معرض الصور إطلع على كل التحديثات 18 صور عن 135 üçgeni من عند 18 المستخدمين 22,522,5135 özel üçgeni , 135 dereceli özel üçgen soru çözümü , 135 30 15 üçgenini açıklayabilir misiniz Eodevcom, Dik ve
Dik Ve Ozel Ucgenler 1
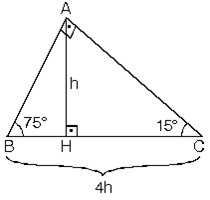
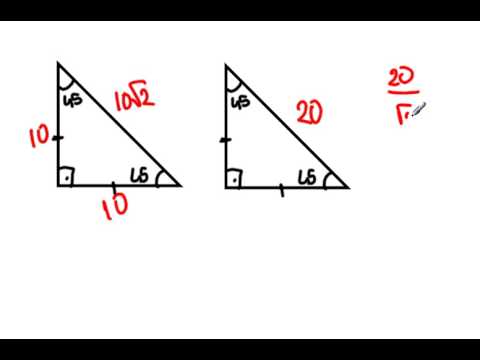
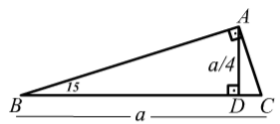
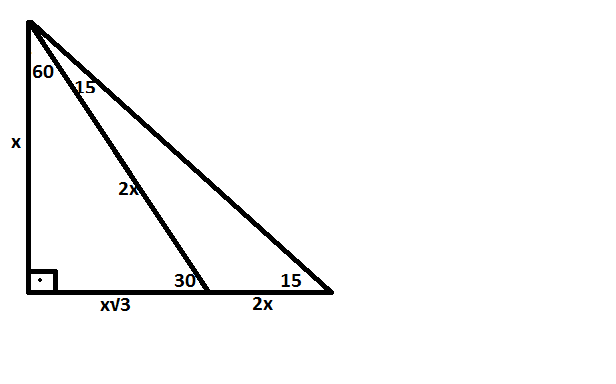
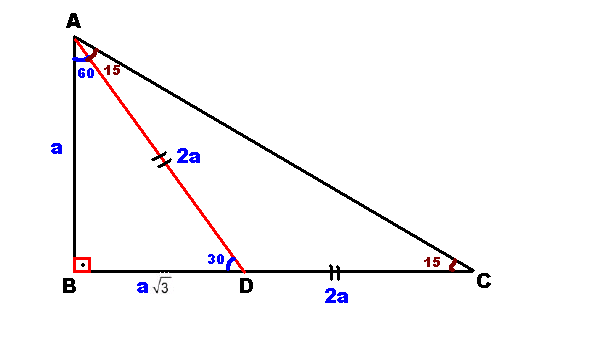
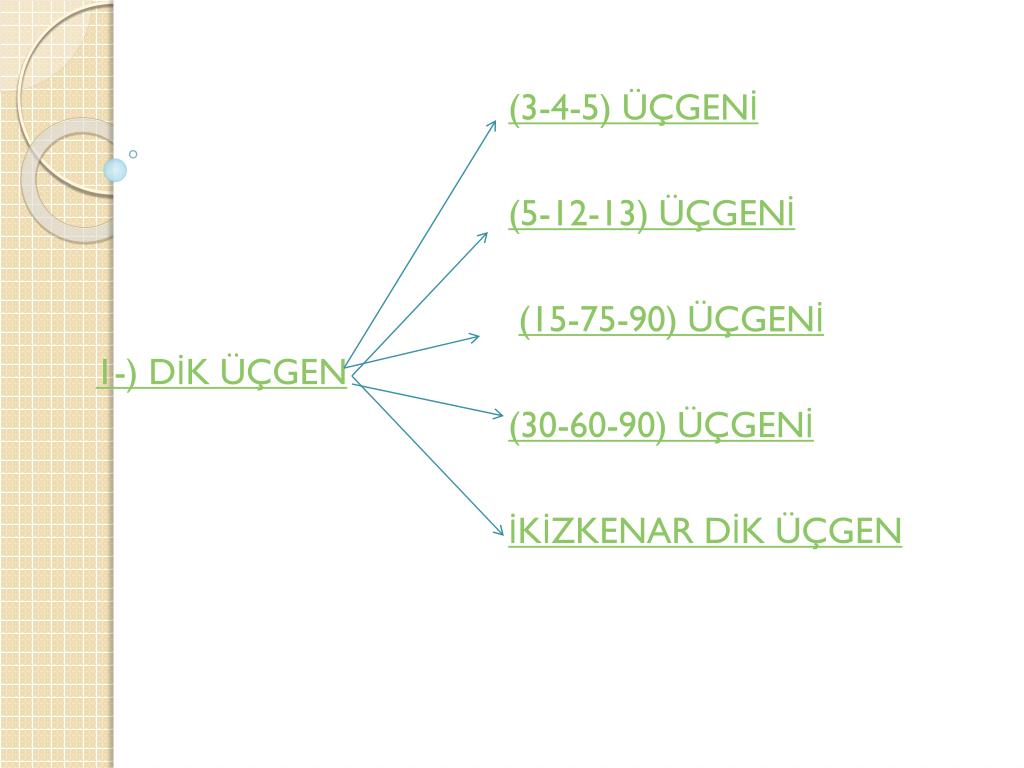
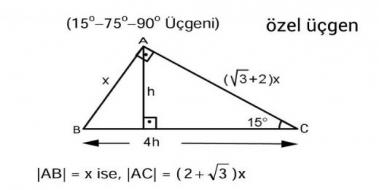
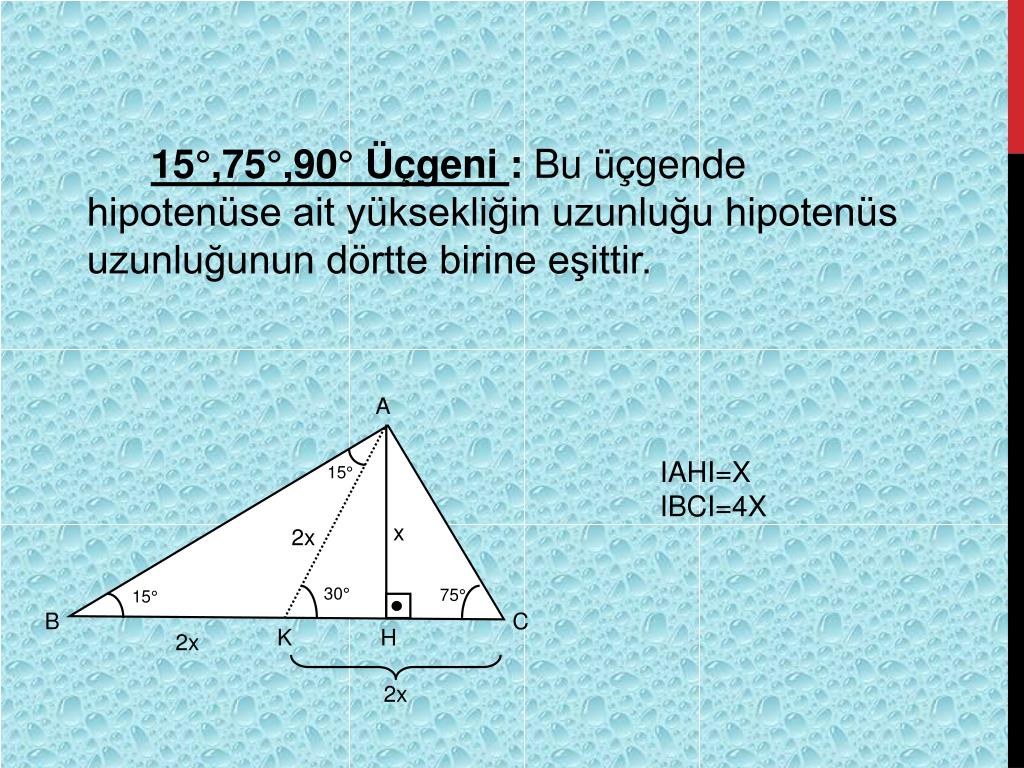
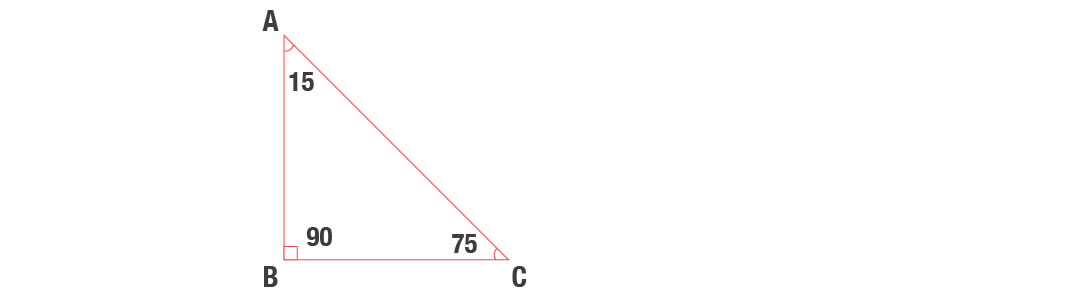
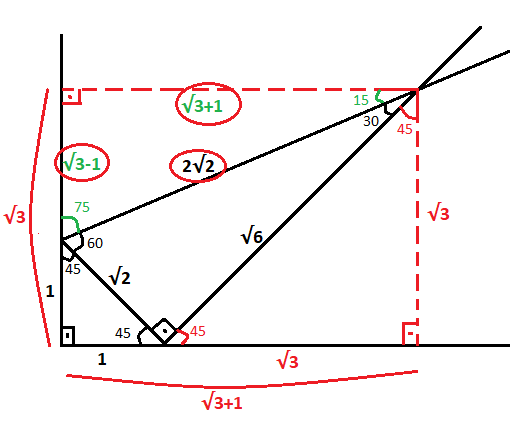
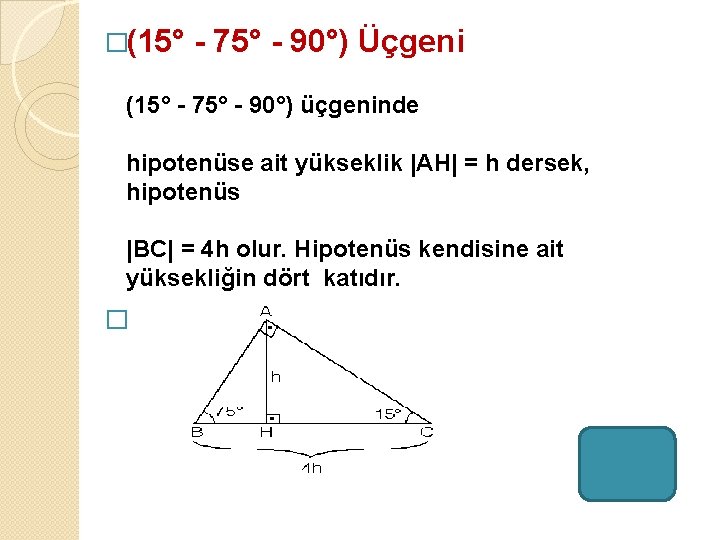
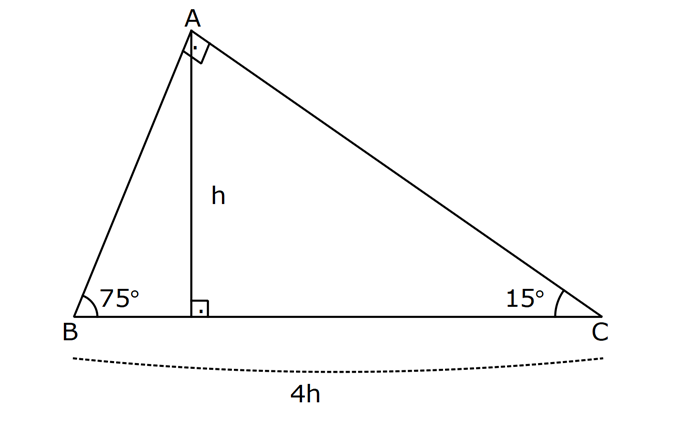
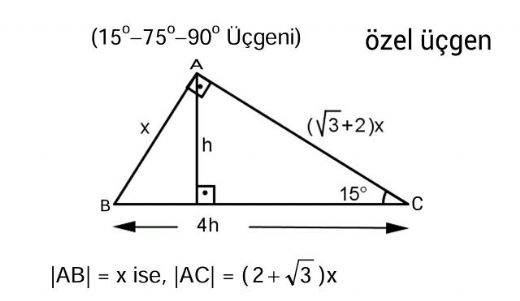
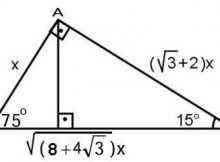
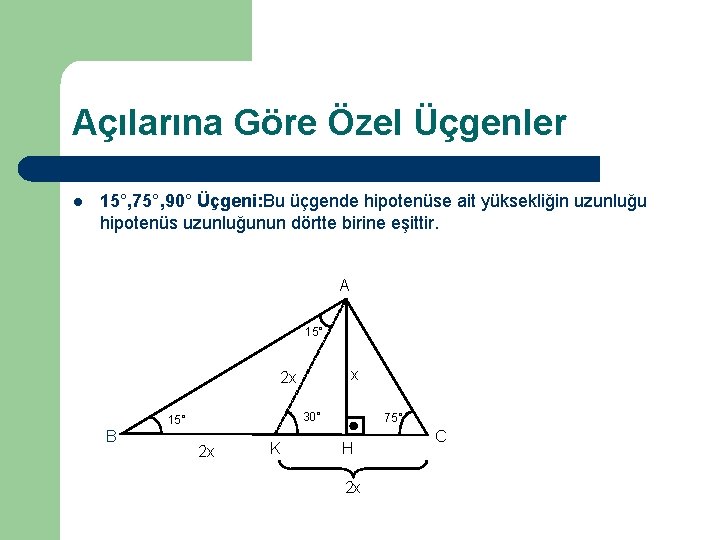
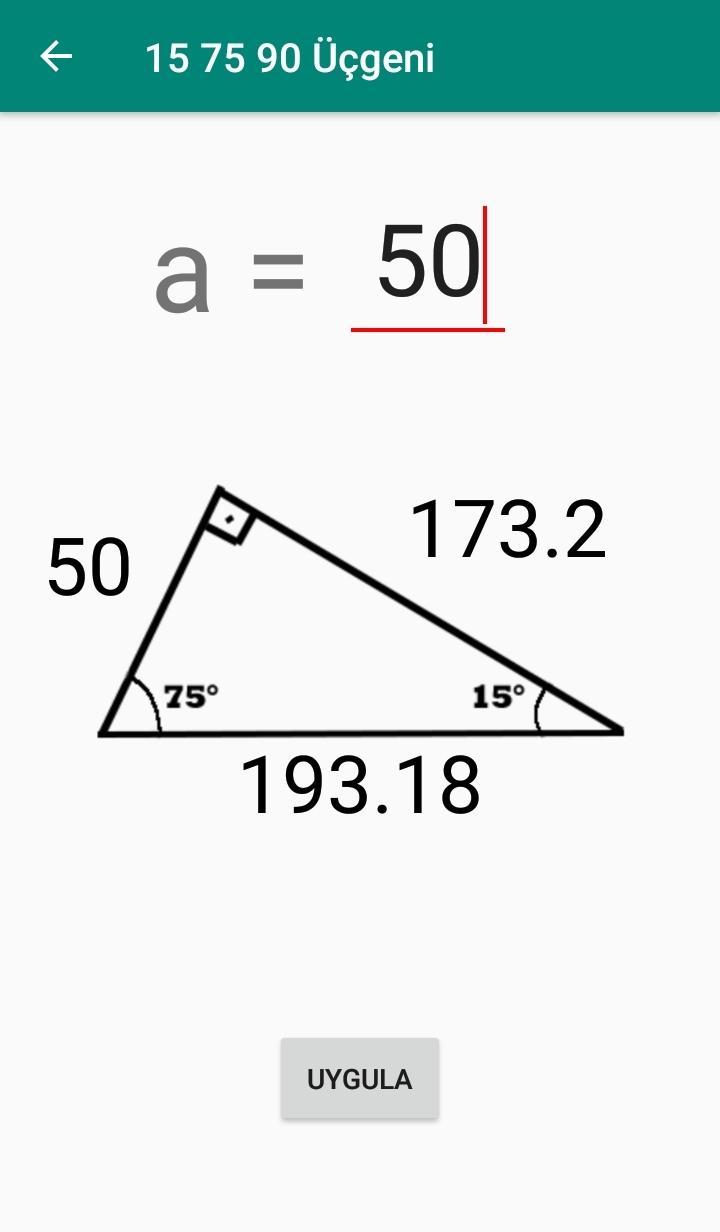
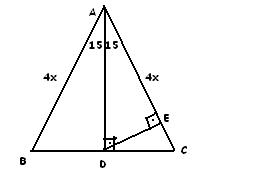
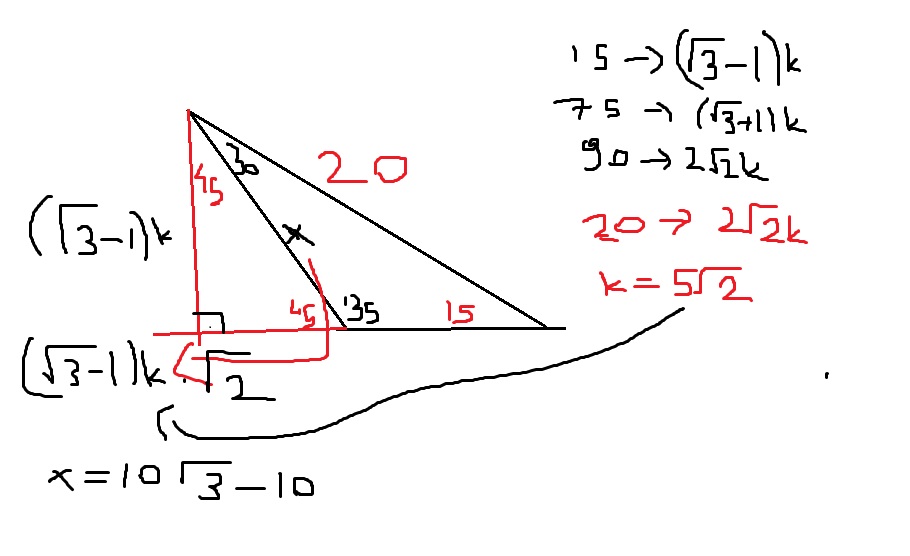
1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır Haberin Devamı İkizkenar ÜçgenTeoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmasıdır Üçgenlerin 3 adet kenarı ve 3 adet Bu özel üçgende yüksekliğin 4 katı bize hipotenüsü vermektedir Yani, hipotenüse inen yükseklik ile 4'ü çarptığımızda ortaya çıkan sayı tekrar hipotenüs olarak bulunmaktadır üçgeni diğer açılarına göre üçgenlerden farklıdır üçgeni bir dar açılı üçgene örnek olarak verilebilir
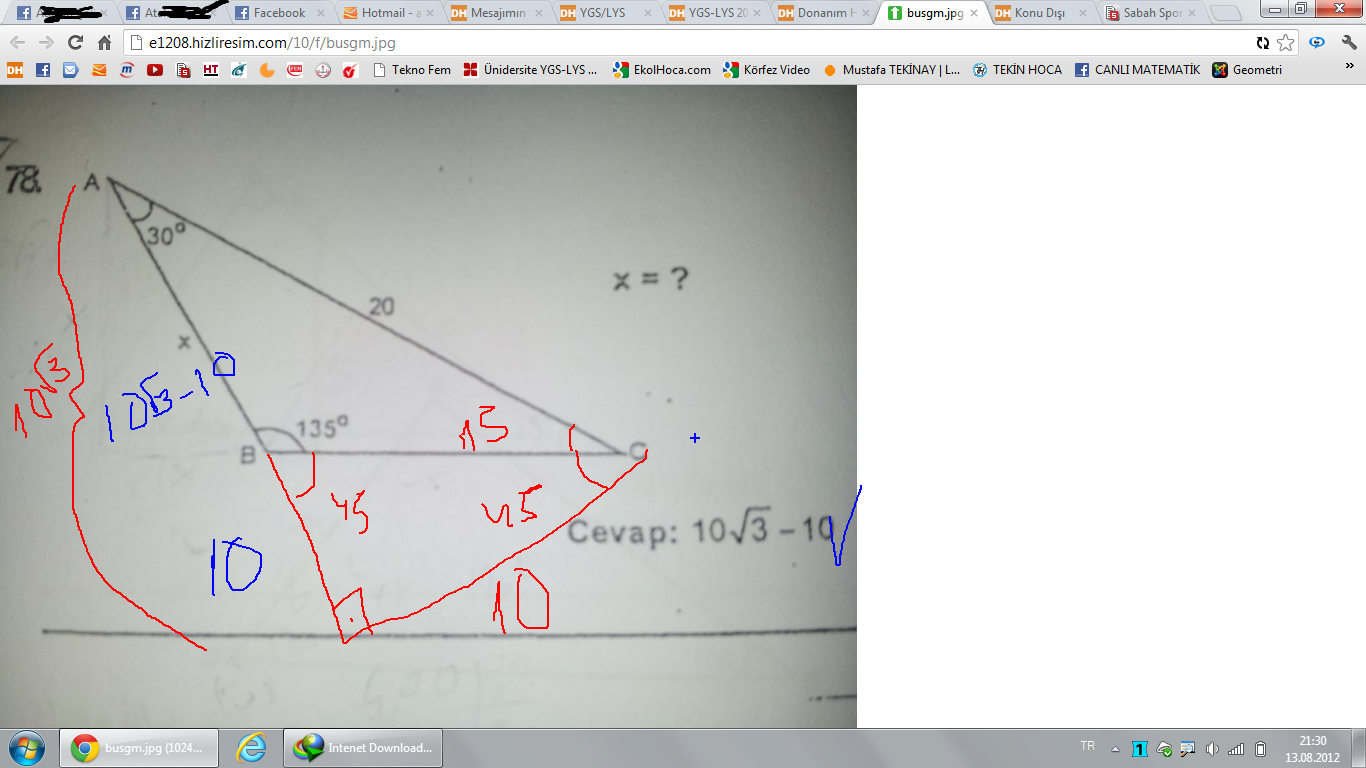
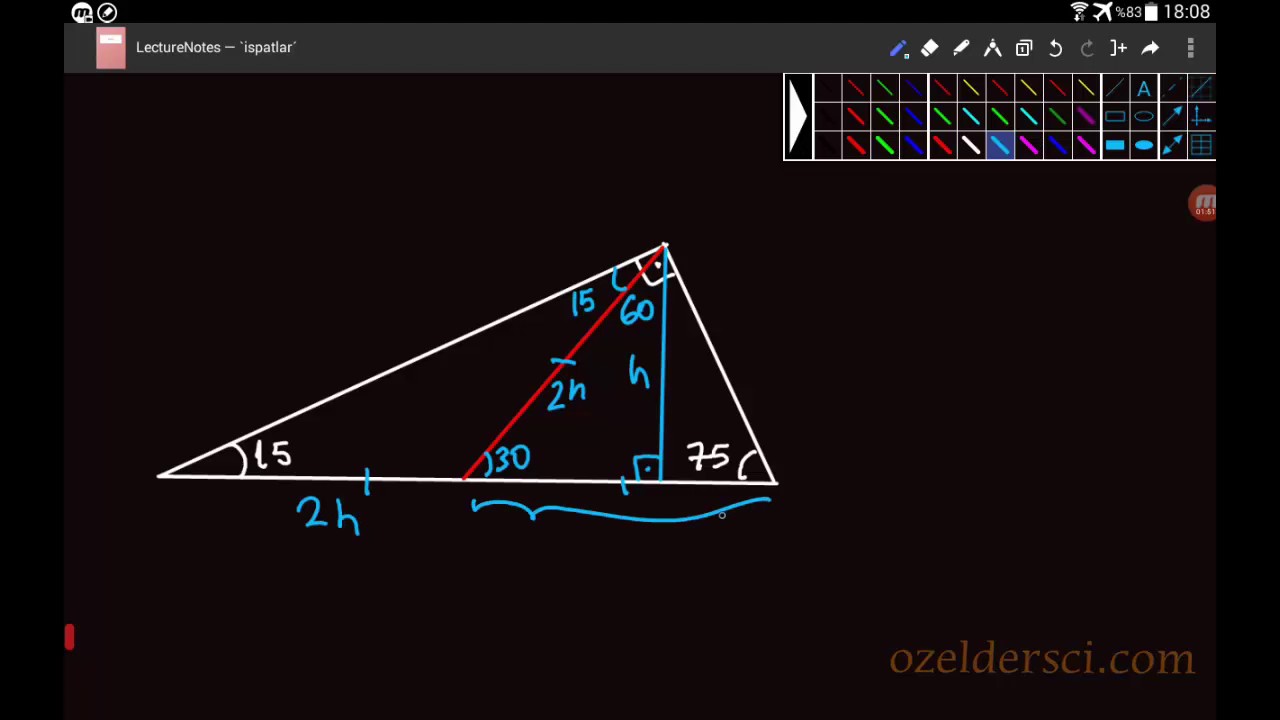
15 75 90 Üçgeni Kuralı Nedir? Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni Enes Ergel bu konuyu 9 sınıf matematik soruları forumunda açtı Cevap 2 Son mesaj 12 15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgendir İkizkenar üçgende birbiriyle aynı açıya ve kenar uzunluğuna sahip olması gerekir
75 15 üçgeniのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | 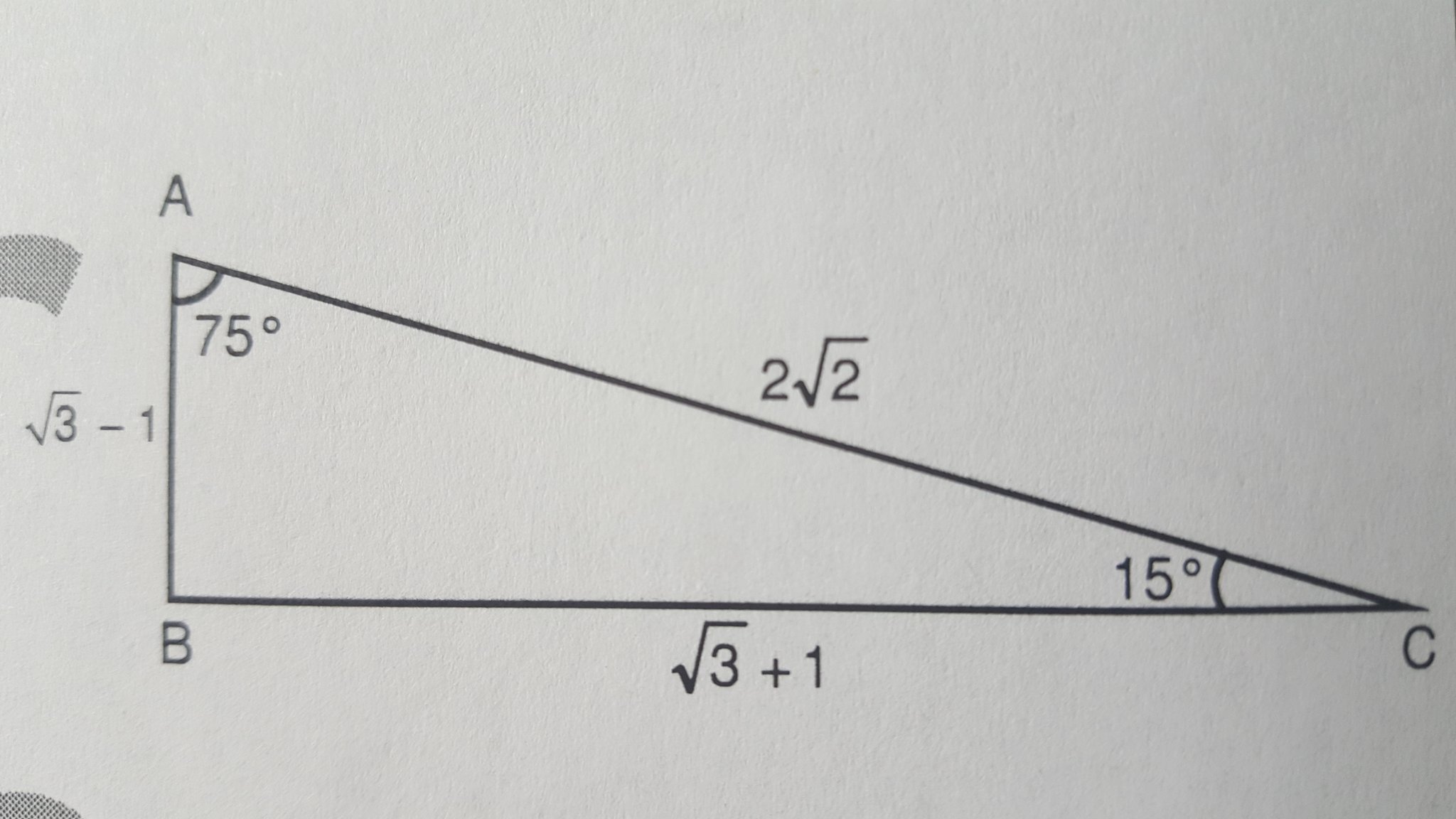 |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 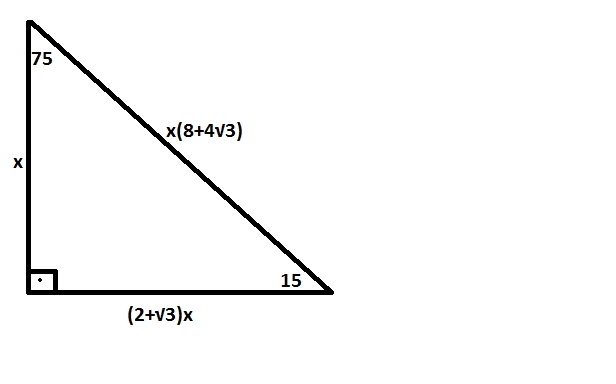 |  |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 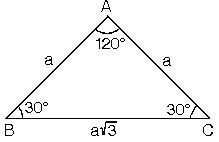 |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「75 15 üçgeni」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
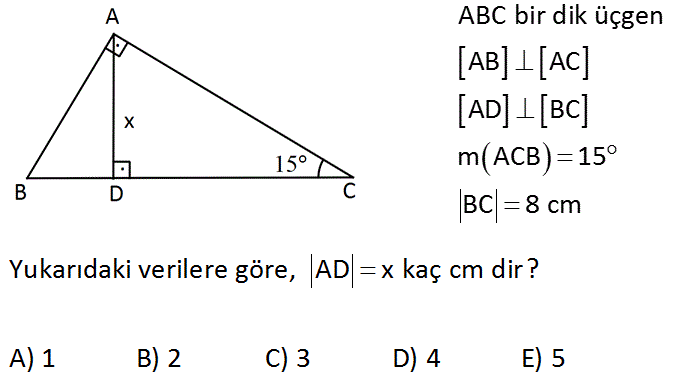
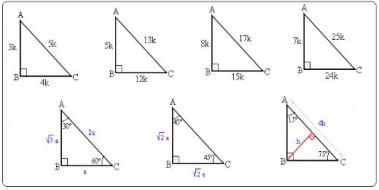
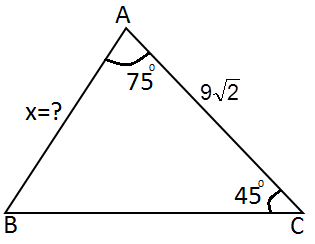
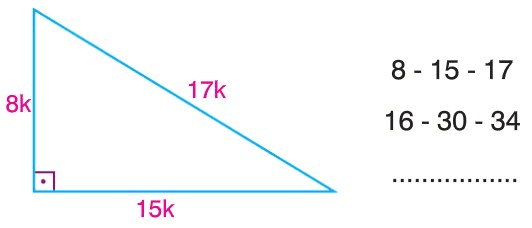
Dik ve Özel Üçgenler Test2 TYTAYT Geometri konuları dik ve özel üçgenler test2 ve çözümleri 30 60 90 üçgeni soruları, 45 45 90 üçgeni ile ilgili sorular, 15 75 90 üçgeni soruları, diklik merkezi soruları, muhteşem üçlü soruları, özel üçgen soru, pisagor bağıntısı soruları, 30 60 90 üçgeni çözümlü sorular, diklik merkezi soru çözümü, 15 75 90Geometri konuları dik üçgenler, özel üçgenler, 30 60 90 üçgeni, 45 45 90 üçgeni, 15 75 90 üçgeni, 15 30 135 üçgeni, öklid, pisagor, muhteşem üçlü, kenarlarına ve açılarına göre özel üçgen soruları Görselleri inceleyebilir, sayfa sonundan PDF formatındaki 11 Sınıf dik ve özel üçgenler test1 dosyasını
コメント
コメントを投稿